Sep 12, 2024
Zero Knowledge proof systems like zk-SNARKs are required to run large field arithmetic operations on points of an elliptic curve over a finite field to generate proofs that the verifiers will use in a blockchain system. One specific component of this process that dominates the proof generation stage is the Multi-Scalar Multiplications, commonly known as MSMs. zk-SNARKs typically spend about 65–80% of the proof generation time on computing MSMs. This opens avenues to leverage FPGAs to accelerate the MSM stage and push towards generating faster proofs. This blog post will briefly discuss how Arithmic is implementing FPGAs to accelerate the proof system.

What are FPGAs?
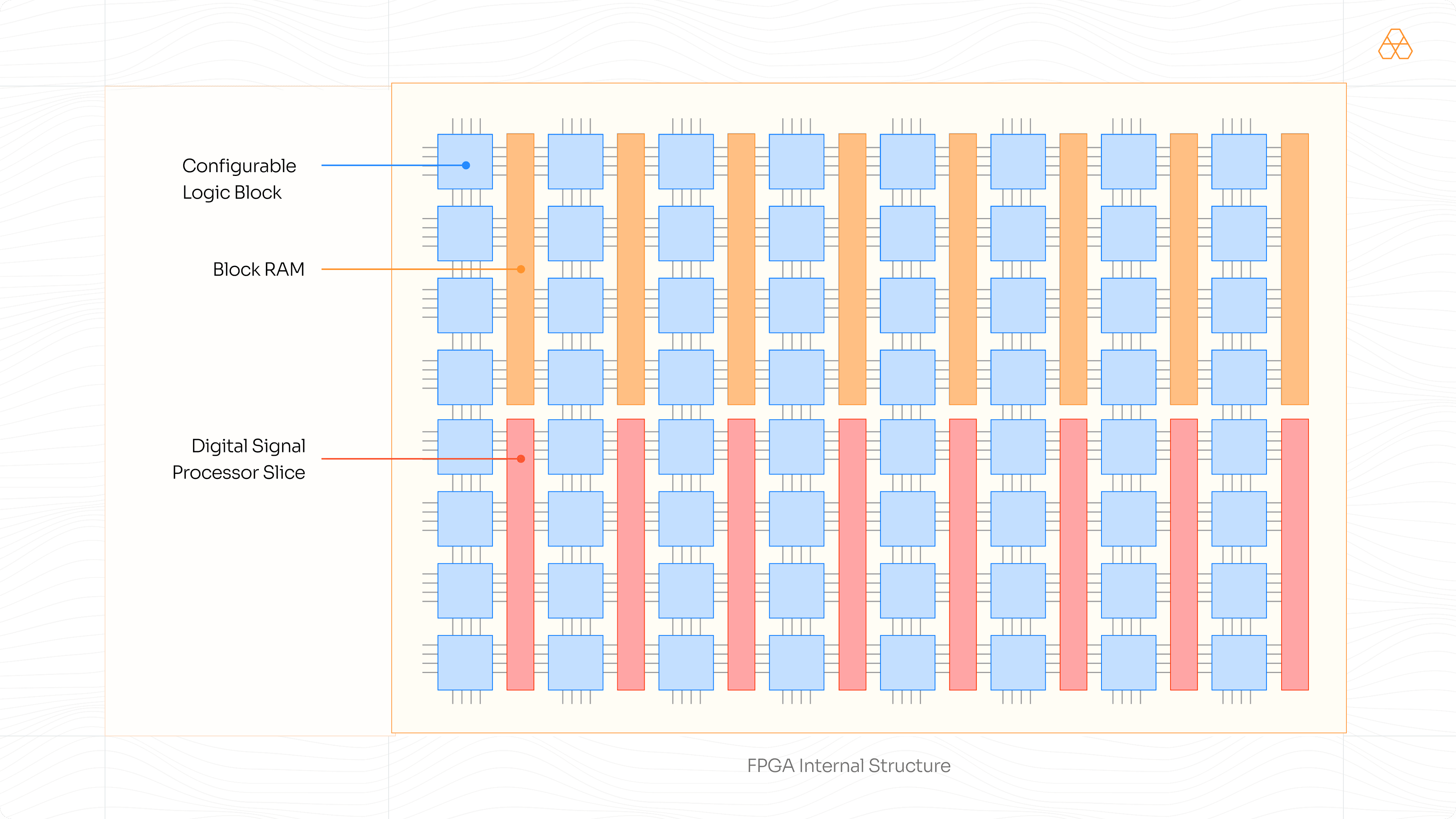
Field Programmable Gate Arrays (FPGAs) are devices that consist of reconfigurable hardware blocks, digital signal processor (DSP) slices and block memory slices which can all be configured by a developer to imitate a logic gate-like digital circuit. Think of FPGAs as programmable microcontrollers, but instead of being able to write software to perform computations, one can design the hardware to perform the computation. To perform an addition, for instance, the user can design any adding logic and configure the FPGA to perform it. At Arithmic, we are leveraging this property of the FPGA to accelerate the MSM stage.
Your brand’s front page has totally different goals. It should show off your brand’s personality, let people explore different features, find blogs and support articles, or even apply for a job. But they won’t necessarily purchase your product from the front page. And that’s why we need landing pages.
Since landing pages are tied to specific campaigns, you don’t need to worry about users lacking information about your product. They arrived at your landing page because they were interested in an ad or post on Google, Bing, YouTube, Facebook, Instagram, Twitter, or similar places on the web. With super detailed campaigns pointing to easy-to-use landing pages, you’re getting high-quality leads that are actually interested in using your product.
What are Multi-Scalar Multiplications?
As the name suggests, multiple scalars need to be multiplied with multiple points over an elliptic curve. These scalars are integers modulo a certain prime number chosen for the particular curve equation. This operation involves calculating the following:

This MSM operation is quite an intensive task to compute on a CPU when attempting to compute it naively. This is because it is an operation performed on large sets of big-integer (> 64-bit) points and scalars. A single operation can take several minutes to compute on top-of-the-line server-grade CPUs. Consequently, this is not a feasible way to construct scalable solutions that can cater to thousands of users at high speeds. Therefore, the MSM operation requires it to be broken down into smaller chunks to make the computation simple, parallelizable and more computationally efficient.
Bucket Method to perform MSMs
To ensure efficient computation on the FPGA, we use the bucket method to break down the MSM operation where we run them in smaller “buckets”. In this method, the points and scalars are split up into windows and then aggregated into buckets. In these buckets, we can perform all the partial modular operations but on smaller bit-width inputs. Consequently, we can have multiple buckets performing partial computations and finally, we can add all the partial outputs to get the final MSM output. This method works best since the FPGAs work efficiently with parallel configured modules.
What has Arithmic developed?
We are developing an MSM accelerator that can be configured on the FPGA and deployed on on-premise servers. The FPGA communicates with the host processor and memory via the PCIe and XDMA protocols to pick up data required to be computed i.e. the elliptic curve points and scalars for MSM in this case.
The reason why FPGAs are best suited for this objective is that they allow the development of various hardware blocks and perform design-space exploration to fetch the best performance-to-power metric. This is crucial as the end goal is to have a hyper-fast accelerator fabbed out in an ASIC chip. Additionally, the reconfigurable nature of the FPGA helps with trial-and-error of hardware modules without the expensive financial overheads of fabricating an ASIC whilst retaining the ability to run tests on silicon.
What does it take to build an MSM accelerator?
To build and deploy an accelerator on an FPGA, we are first required to design individual modules (or the entire behavioural system) that are required to perform the computations. For MSMs, since they primarily consist of arithmetic operations, designing fast arithmetic modules such as adders and multipliers using computationally efficient algorithms is crucial. Since these MSMs involve field elements that span over a large bit-width (> 64 bits), they need to be optimized to ensure that the FPGA resources are efficiently used. Since these are large bit-width arithmetic modules, the DSP(digital signal processor) resources of the FPGA are heavily used. The reason behind this is that the DSP resources offer fast arithmetic modules that can be cascaded to perform such large bit-width arithmetic. For instance, an elliptic curve adder would take up almost 50% of the DSP slices (the FPGA used here is the Xilinx Alveo U55N) leaving just another 50% for the rest of the modules. The system architects must be mindful of setting up the modules in such a way that the FPGA fabric is maximally utilized, with minimal inter-module communication overhead and optimal performance.
Future Plans at Arithmic
At Arithmic, the end goal for hardware solutions is to develop ASICs for zero-knowledge-proof systems. This accelerator project is the first stepping stone towards achieving that vision. The Arithmic team will continue working on optimizing and extending this accelerator to other parts of the zkVM on a single FPGA for the foreseeable future. We are determined to use multiple FPGAs and get exponentially better performance metrics for computing MSMs and potentially other intensive tasks of the proof system.

Links:
X handle: https://x.com/ArithmicNetwork
